
-

Khai cuộc (phần 4): Một số bẫy khai cuộc cờ vua thông dụng (tiếp theo)
[18-08-2021]
Tiếp theo phần 3 của chủ đề khai cuộc cờ vua, chúng ta đến với hai bẫy thông dụng trong các khai cuộc thoáng.
-

Khai cuộc (phần 3): Một số bẫy khai cuộc thông dụng
[16-08-2021]
Đối với người mới học chơi cờ vua, nắm vững nguyên tắc khai cuộc và tránh phạm sai lầm trong việc ra quân là chưa đủ vì có những thế biến
-

Khai cuộc (Phần 2): Các sai lầm trong việc phát triển quân
[20-07-2021]
Việc thực hiện đúng các nguyên tắc khai cuộc giúp ích rất nhiều cho những kỳ thủ nhỏ tuổi hoặc mới làm quen với cờ vua.
-

Khai cuộc (PHẦN 1): Các nguyên tắc khai cuộc
[27-06-2021]
Khai cuộc là giai đoạn đầu tiên của ván cờ và giữ vị trí quan trọng trong việc hình thành thế trận cũng như kế hoạch chơi về sau.
-

Bài 5: Khai cuộc nữa thoáng
[22-05-2015]
Các đấu thủ nhỏ thường đánh kém mỗi khi chơi quân Đen với nhiều lý do. Một phần là vì tâm lý phòng thủ khi phải đi sau nhưng có một lý do mà ít ai để ý tới, khai cuộc thoáng với trung tâm chốt đối xứng (cố định) e4-e5 luôn mang lại cho Trắng ít nhiều ưu thế.
-

Bài 4: Ván cờ Ý yên tĩnh và sôi động (phần 2)
[13-05-2015]
Ý tưởng chính của Gambit Evans là hy sinh chốt b để chiếm trung tâm, khai thác đường chéo a2 – g8 (đánh vào chốt f7), ra quân nhanh nhất có thể để tấn công Vua Đen tại trung tâm.
-
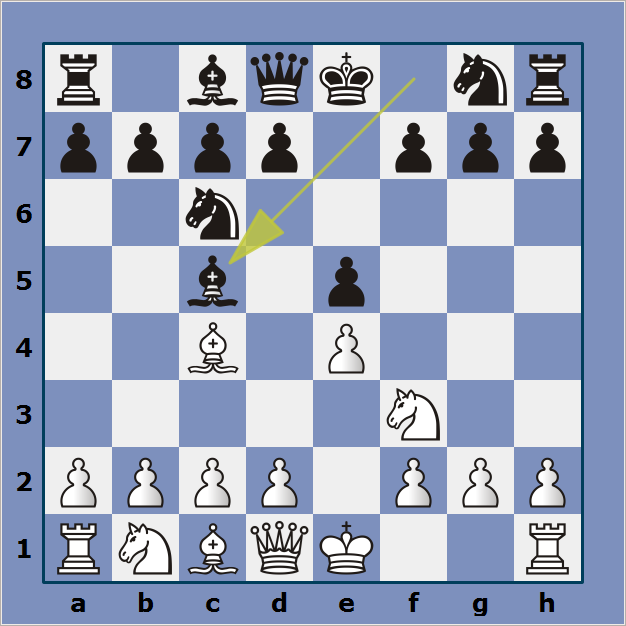
BÀI 3: Ván cờ Ý yên tĩnh và sôi động (phần 1)
[08-05-2015]
Ván cờ Ý (còn có tên gọi khác là Giuoco Piano) được xem là khai cuộc lâu đời nhất được ghi nhận cho đến nay.
-

Bài 2 : Khai cuộc thoáng
[27-10-2014]
Các khai cuộc với nước bắt đầu của hai bên là 1.e4 e5 được gọi là khai cuộc thoáng. Đây là loại khai cuộc mà người mới học chơi cờ nên tập luyện vì phù hợp với kỳ thủ ở trình độ chưa cao
-

Bài 1: Tổng quan về khai cuộc
[27-10-2014]
Khai cuộc là phần đầu tiên của một ván cờ và có ý nghĩa cực kỳ quan trọng trong việc định hình thế trận, lối đánh của hai bên.

